给定一个数组，每个元素代表跳跃的距离，判断是否能从起点出发，跳到数组的末尾。

例如：给定一个数组[3，7，8，1，5]，从起点出发，可以跳跃3步，跳到位置3，然后跳1步，跳到位置4，跳4步到达末尾。

思路分析

• 定义一个变量，用来初始化当前能到达的最远位置。
• 遍历数组，获取当前位置索引及值，这里使用到 enumerate 函数,用来实现能够同时获取到当前位置及值。
• 若当前位置超出了能够到达的最远位置，则无法继续跳跃。
• 使用 max 数更新 最远距离 ，确保它总是表示当前能到达的最远位置。
• 遍历完成后，检查 max_distance 是否至少为数组长度减一，即是否能到达最后一个位置。

enumerate简述

Python内置的一个函数，用于将一个 可遍历 的数据对象（如 列表、元组或字符串 ）组合为一个 索引序列，同时列出数据和数据下标 ，一般用在for循环当中。 enumerate 返回的是一个 枚举对象 ，它包含元组，每个元组包含两个元素，一个是索引值，一个是原始数据值。

举例：

for index, value in enumerate(['a', 'b', 'c']):  
    print(f"Index: {index}, Value: {value}")

输出结果：

Index: 0, Value: a  
Index: 1, Value: b  
Index: 2, Value: c

贪心算法简述

贪心算法是在每一步选择中都采取在当前状态下 最好或最优（即最有利） 的选择，从而希望导致结果是全局最好或最优的算法。是从问题的某一个初始解出发逐步逼近给定的目标，以尽可能快地求得更好的解。并且希望通过所做的局部最优选择来导致最终的全局最优解时，这样的算法就被称为贪心算法。

在 canJump 函数中，贪心策略体现在每一步都更新 max_distance 为当前位置能够到达的最远距离。这意味着在每一步，算法都在尽可能地扩大能够到达的范围。

代码实现

def Jumping_Game(nums):
    max_distance = 0  # 记录当前能够到达的最远位置
    for i, jump in enumerate(nums):  # 遍历数组，获取当前位置的索引和跳跃长度
        if i > max_distance:  # 如果当前位置超出最远能够到达的位置，则无法继续跳跃
            return False
        if i + jump >= len(nums) - 1:  # 如果能够到达或超过最后一个位置，则返回True
            return True
        max_distance = max(max_distance, i + jump)  # 更新最远能够到达的位置
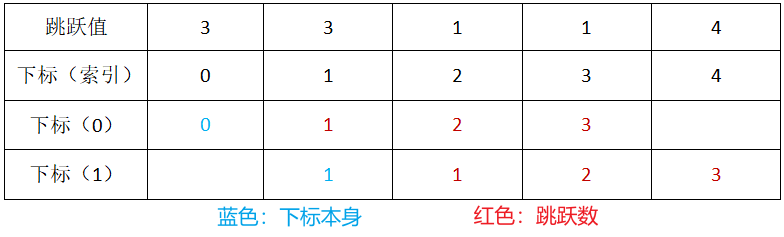
    return False  # 遍历完数组后仍未到达最后一个位置，返回False

测试用例详述

测试用例一：list_nums = [3, 3, 1, 1, 4]

• 从位置0开始，数值是3，意味着可以跳到位置0、1、2、3。
• 一旦到达位置1，发现从这个位置也可以跳跃的最大步数是3，这意味着可以直接跳到位置4（因为 1 + 3 >= 4 ）。在这种情况下，我们不需要遍历位置2或位置3，已经找到了一条从位置0到位置4的路径。

图例（表格方式，红色为跳跃数）：

测试用例二：list_nums2 = [3, 2, 1, 0, 4]

• 同样从位置0开始，数值是3，我们可以跳到位置0、1、2、3。
• 更新 max_distance 为3。
• 在位置1，数值是2，我们可以跳到位置1、2、3。此时 max_distance 仍然是3。
• 在位置2，数值是1，我们只能跳到位置2或3。此时 max_distance 仍然是3。
• 在位置3，数值是0，这意味着我们无法从这里跳到更远的位置。此时， i （当前位置）已经大于 max_distance （最远能够到达的位置），所以函数返回 False .

图例（表格方式，红色为跳跃数）：

总结

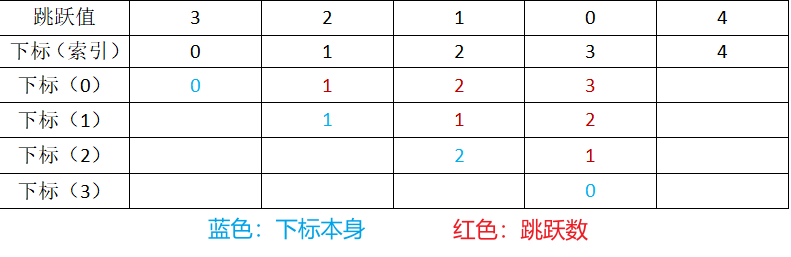
关键在于每一步都尽可能地更新 max_distance ，从而确保我们不会错过任何可能到达数组的末尾路径。

时间复杂度： O(n) ，代码遍历了数组nums一次，没有嵌套循环或其他会增加时间复杂度的操作。因此，时间复杂度是O(n)，其中n是数组nums的长度。

空间复杂度： O(1) ，代码中只使用了几个变量（如max_distance和i，jump）来追踪当前能够到达的最远位置,当前下标，当前位置的值。这些变量不随数组nums的大小变化而增加，因此空间复杂度是O(1)。