算法金 | 突破最强算法模型！！学会随机森林，你也能发表高水平SCI

来源：网络更新时间：2024-06-02 04:32:29

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

就在去年下半年，如果你在 Google Scholar 上以 "Random Forest" 为关键词进行检索，并按时间排序：

你会看到这种方法被广泛应用于各个领域的研究，包括 GIS、环境科学和遥感等。发表的期刊涵盖了从《Frontiers》到《Remote Sensing》（MDPI）以及《环境科学》期刊等。有不少中上水平的期刊，覆盖从一区到四区。为什么这种方法始终受到欢迎？

1.1 什么是随机森林算法

随机森林算法是一种集成学习方法，通过构建多个决策树来提高模型的准确性和稳定性。

1.2 随机森林算法的应用领域

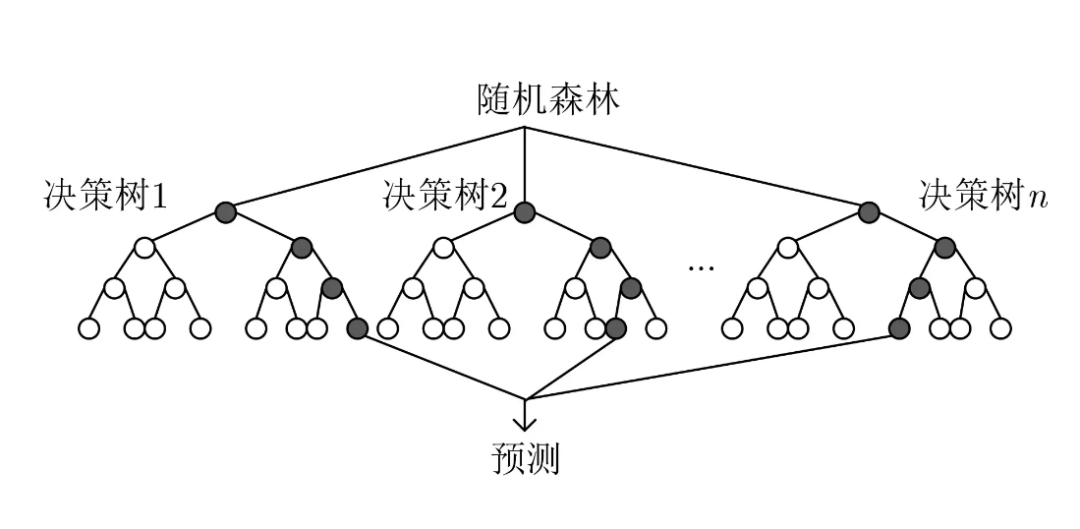
随机森林算法在许多领域有广泛的应用，包括：

金融：信用评分、风险预测
医疗：疾病预测、诊断辅助
营销：客户分类、市场细分
生物信息学：基因表达数据分析
环境科学：生态系统建模、气候变化研究

2. 随机森林的基本概念

2.1 决策树概述

决策树是一种树形结构的模型，用于进行分类和回归任务。它通过一系列的决策节点将数据集划分为更小的子集，直到所有数据都被正确分类或达到了最小叶节点的要求。每个节点代表数据集中的一个特征，每个分支代表这个特征的可能取值，每个叶节点代表最终的分类结果或回归值。

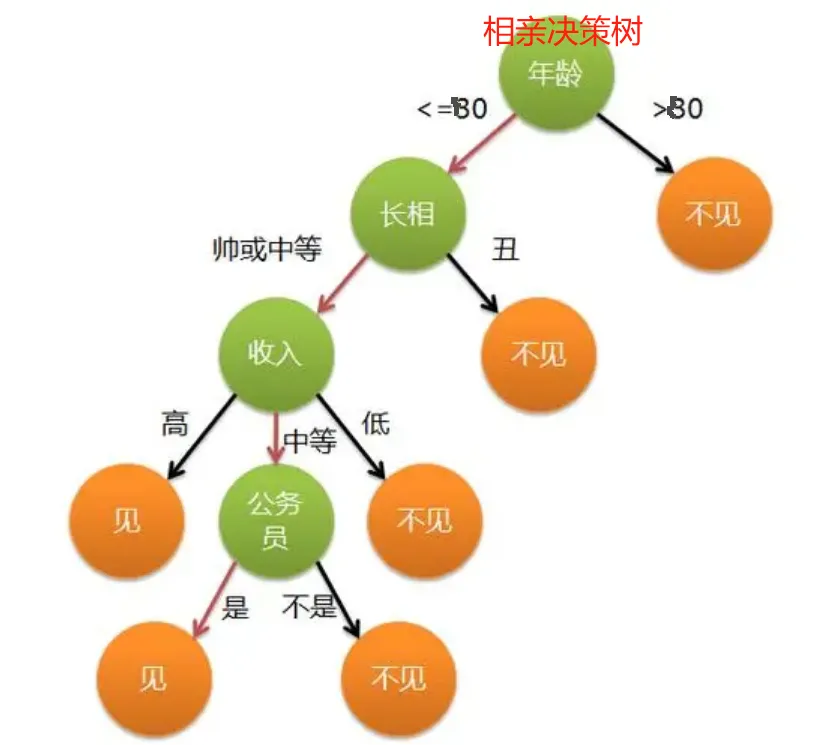
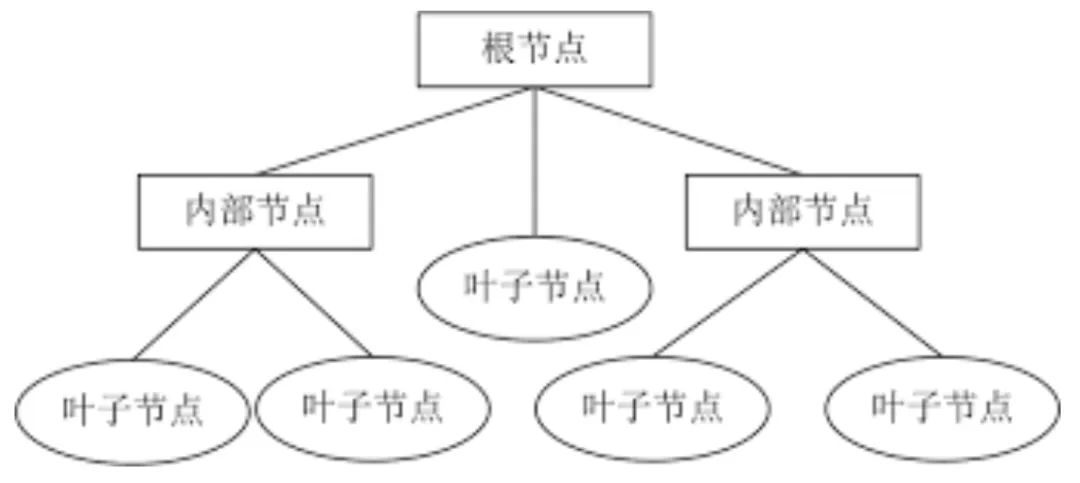
决策树的优点：

简单直观，易于理解和解释
可以处理数值型和分类型数据
可以处理缺失值和不均衡数据

决策树的缺点：

容易过拟合
对于微小数据变化敏感

2.2 随机森林的定义

随机森林是一种集成学习方法，通过构建多个决策树来提高模型的准确性和鲁棒性。每棵树都是在不同的子数据集和特征子集上训练的，最终的预测结果是所有树的预测结果的平均值（回归问题）或多数表决（分类问题）。

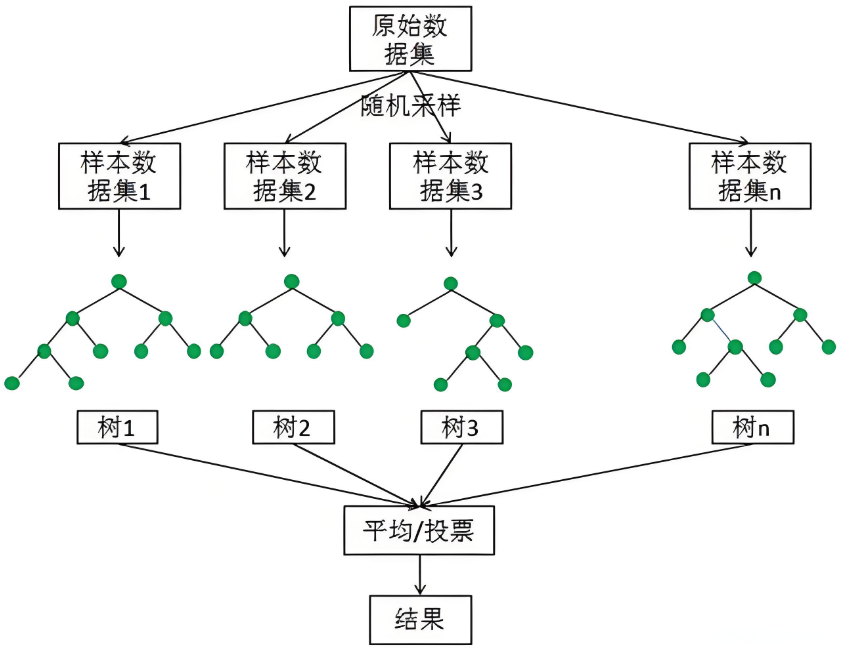
2.3 随机森林的优点和缺点

随机森林的优点：

高准确性：通过集成多个决策树，减少单一模型的过拟合现象，提高预测的准确性。
鲁棒性：对数据中的噪声和异常值不敏感。
处理高维数据：能够处理具有大量特征的数据集。
并行处理：可以并行训练多个决策树，提高计算效率。

随机森林的缺点：

模型复杂性：由于包含大量决策树，模型可能会变得非常复杂。
训练时间长：训练多个决策树需要更多的时间和计算资源。
可解释性差：相比单一决策树，随机森林的模型较难解释。

3. 随机森林的工作原理

3.1 集成学习的概念

集成学习是一种通过结合多个模型的预测结果来提高整体预测性能的方法。它的基本思想是将若干个基学习器（如决策树）结合起来，从而获得一个性能优于任何单一基学习器的模型。常见的集成学习方法包括 Bagging、Boosting 和 Stacking。

3.2 Bagging 技术

Bagging，全称为 Bootstrap Aggregating，是一种通过对训练数据进行重采样来生成多个子数据集的方法。每个子数据集都用于训练一个基学习器，最终的预测结果通过所有基学习器的预测结果进行平均（回归问题）或多数表决（分类问题）得到。Bagging 可以有效降低模型的方差，减少过拟合。

Bagging 的步骤：

从原始数据集通过有放回抽样生成若干个子数据集。
在每个子数据集上训练一个基学习器。
对新数据进行预测时，将所有基学习器的预测结果进行平均或多数表决。

3.3 随机子空间法

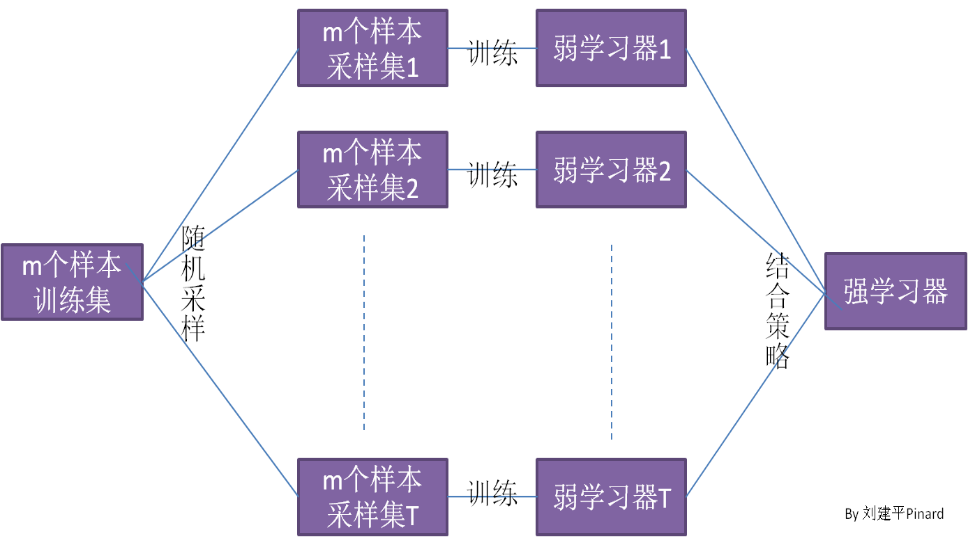
随机子空间法是一种在每次分裂节点时随机选择特征子集的方法。传统的决策树在分裂节点时会考虑所有特征，而随机子空间法则仅选择一部分特征，从而增加了模型的多样性。

随机森林结合了 Bagging 和随机子空间法，即在构建每棵决策树时：

通过 Bagging 方法生成不同的子数据集。
在每个节点分裂时，随机选择一部分特征进行选择。

这种方法不仅降低了过拟合风险，还提高了模型的泛化能力。

4. 随机森林的数学基础

4.1 信息增益和基尼系数

信息增益是衡量一个特征对数据集分类纯度提高程度的指标。信息增益越大，特征的分类效果越好。决策树在每个节点选择特征时，通常选择信息增益最大的特征进行分裂。

信息增益的计算公式：

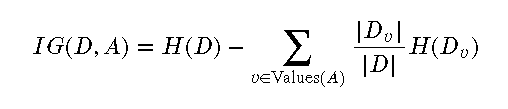
基尼系数是另一种衡量分类纯度的方法，基尼系数越小，纯度越高。决策树在每个节点选择特征时，也可以选择基尼系数最小的特征进行分裂。

基尼系数的计算公式：

4.2 多样性和独立性

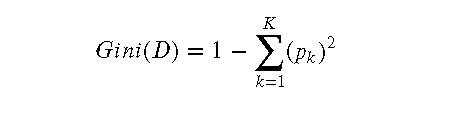
随机森林通过引入多样性和独立性来提高模型的性能。通过对数据集进行重采样（Bagging）和对特征进行随机选择（随机子空间法），每棵树都在不同的数据和特征子集上训练，从而提高了模型的鲁棒性和泛化能力。

4.3 随机森林中的数学公式

随机森林的预测结果是所有决策树的预测结果的平均值（回归问题）或多数表决（分类问题）。假设有 ?? 棵决策树，每棵树的预测结果为 ℎ?(?)ℎ?(?)，则随机森林的最终预测结果 ?(?)?(?) 为：

分类问题：

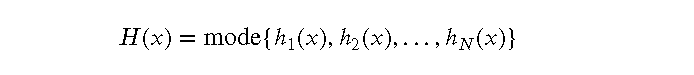
回归问题：

5. 随机森林的代码示例

5.1 使用 scikit-learn 实现随机森林

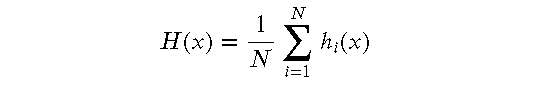
我们将使用 scikit-learn 库来实现随机森林，并展示其在分类问题中的应用。我们将使用一个自制的包含武侠元素的数据集。

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np

# 生成一个包含武侠元素的模拟数据集
def create_wuxia_dataset():
    np.random.seed(42)
    # 创建分类数据集，增加一些武侠元素的变量（例如内力、轻功、武器）
    X, y = make_classification(n_samples=500, n_features=5, 
                               n_informative=3, n_redundant=0, n_clusters_per_class=1, random_state=42)
    feature_names = ['Neili', 'Qinggong', 'Weapon', 'Experience', 'Strategy']
    return X, y, feature_names

X, y, feature_names = create_wuxia_dataset()

# 划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 初始化随机森林分类器
clf = RandomForestClassifier(n_estimators=100, random_state=42)

# 训练模型
clf.fit(X_train, y_train)

# 预测
y_pred = clf.predict(X_test)

# 评估模型
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy}')

# 可视化特征重要性
importances = clf.feature_importances_
indices = np.argsort(importances)[::-1]

plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align='center')
plt.xticks(range(X.shape[1]), [feature_names[i] for i in indices])
plt.xlabel("Feature")
plt.ylabel("Importance")
plt.show()

5.2 参数调优和模型评估

随机森林有许多可调节的参数，比如树的数量（n_estimators）、每棵树的最大深度（max_depth）等。通过调节这些参数，可以提高模型的性能。

from sklearn.model_selection import GridSearchCV

# 定义参数网格
param_grid = {
    'n_estimators': [50, 100, 200],
    'max_depth': [None, 10, 20, 30],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4]
}

# 使用网格搜索进行参数调优
grid_search = GridSearchCV(estimator=clf, param_grid=param_grid, cv=3, n_jobs=-1, verbose=2)
grid_search.fit(X_train, y_train)

# 最佳参数
print(f'Best parameters found: {grid_search.best_params_}')

# 使用最佳参数进行预测
best_clf = grid_search.best_estimator_
y_pred_best = best_clf.predict(X_test)

# 评估最佳模型
best_accuracy = accuracy_score(y_test, y_pred_best)
print(f'Best Accuracy: {best_accuracy}')

5.3 随机森林的可视化

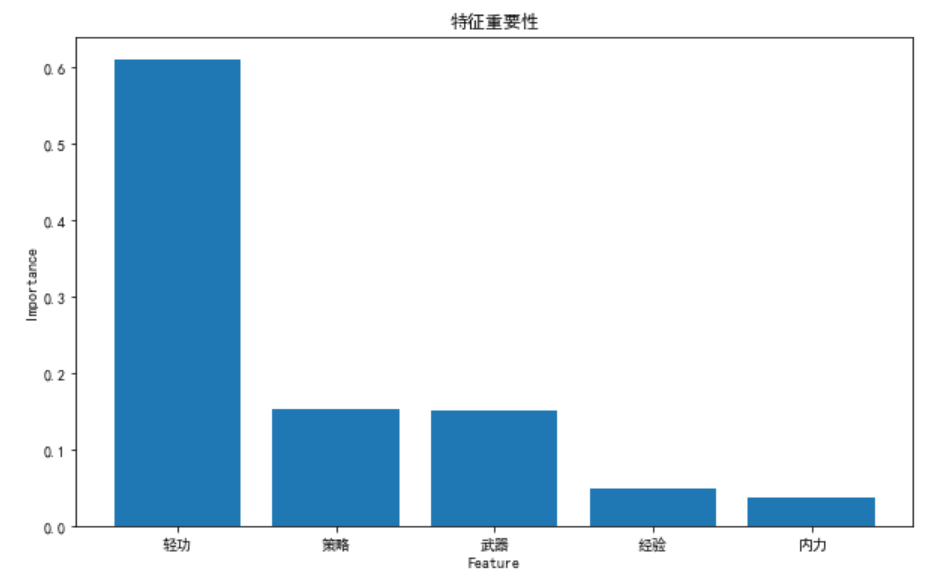
我们可以通过可视化特征重要性来理解模型的决策过程。特征重要性表示每个特征对模型预测的重要程度。

# 可视化特征重要性
importances = best_clf.feature_importances_
indices = np.argsort(importances)[::-1]

plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align='center')
plt.xticks(range(X.shape[1]), [feature_names[i] for i in indices])
plt.xlabel("Feature")
plt.ylabel("Importance")
plt.show()

以上是随机森林的代码示例部分的内容，包含了从模型训练、参数调优到特征重要性可视化的完整流程。