算法金 | 你真的完全理解 Logistic 回归算法了吗

来源：网络更新时间：2024-06-03 15:32:51

大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」

今日 178/10000

1. 引言

吴恩达：机器学习的六个核心算法！，

通透！！十大回归算法模型最强总结，

突破最强算法模型，决策树算法！！

急匆匆把逻辑回归给落下了，今天我们杀他个回马枪，再战三百回合

逻辑回归 Logistic 回归是一种用于分类问题的统计方法。它通过使用逻辑函数（如 Sigmoid 函数）将输入变量的线性组合映射到一个概率值，从而实现分类任务。

Logistic 回归广泛应用于许多领域，主要用于二分类问题，例如：

信用评分：预测借款人是否会违约。
医学诊断：判断某个患者是否患有某种疾病。
市场营销：预测客户是否会购买某产品。
社会学研究：分析某种行为是否会发生。

通过这篇文章，你将深入了解 Logistic 回归的原理、模型构建方法以及如何使用 Python 实现 Logistic 回归模型。

2. 数学基础

2.1 线性回归实现分类

在理解 Logistic 回归之前，我们先回顾一下线性回归。线性回归用于预测连续值，其数学形式为：

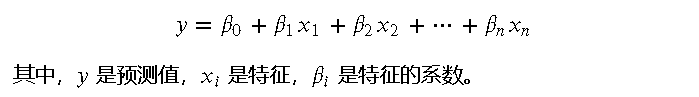
简化演示：比如这样的一个简单的 2 类别样本分布，我们可以最终得到线性方程可视化后的结果可能如下：

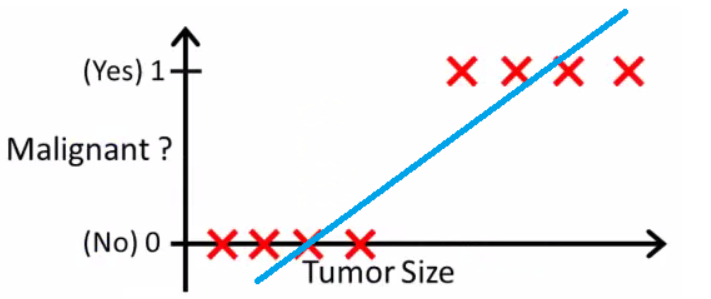
下一步，我们可以把这个线性回归延申到分类任务中，怎么做呢？

我们可以设定一个阈值，大于和小于这个阈值的分别属于两类（等于阈值呢，爱咋咋地，影响不大）
我们可以从下图看到，这个分类结果很完美，完全把两个类别区分开了

2.2 线性回归分类的缺点

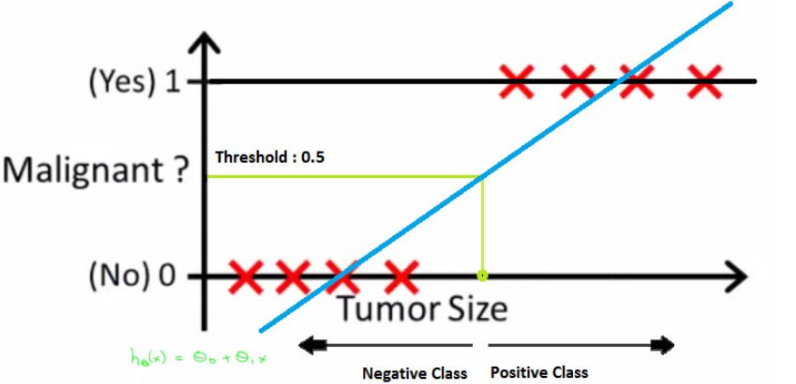
线性回归虽简单有效，但在分类问题中存在局限。线性回归的输出是连续值，而分类问题需要离散的类标签。此外，线性回归不能保证输出值在 0 和 1 之间，这对于概率预测是不合理的。

接着 2.1 的内容，通过对比直观的理解一下线性回归分类的缺点

2.1 描述的回归转分类的方式，在下面场合就不灵了，比如收集数据的小哥哥小姐姐开了个小差，数据中混入一个异常点

这时候分类结果就很不理想了，如下图，如果我们还是使用 0.5 为阈值，那中间几个样本都被分类错了
除非我们更换阈值，问题是设置多少为阈值呢？想想看，这样是不是表现很不稳定

2.3 Logistic 函数（Sigmoid 函数）

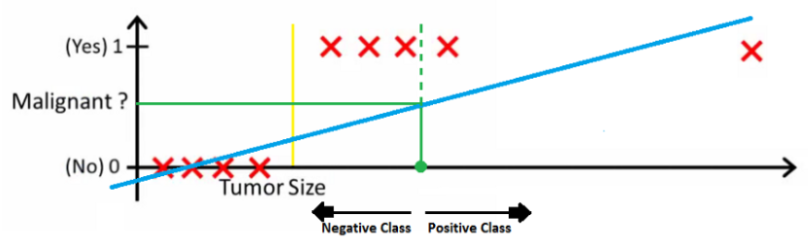
为了解决上述问题，来了

逻辑回归（Logistic Regression，简称 LR）是一种广义线性模型（GLM），通常用于分类问题。与传统的线性回归模型（预测连续值输出）不同，逻辑回归预测的是一个概率值，表示为介于 0 和 1 之间的数。这使得它非常适合于二分类问题

Logistic 回归使用了 Sigmoid 函数，其数学形式为：

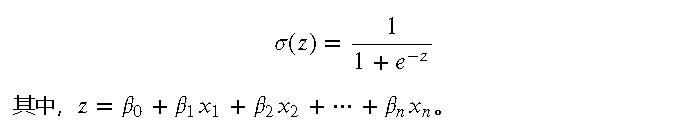
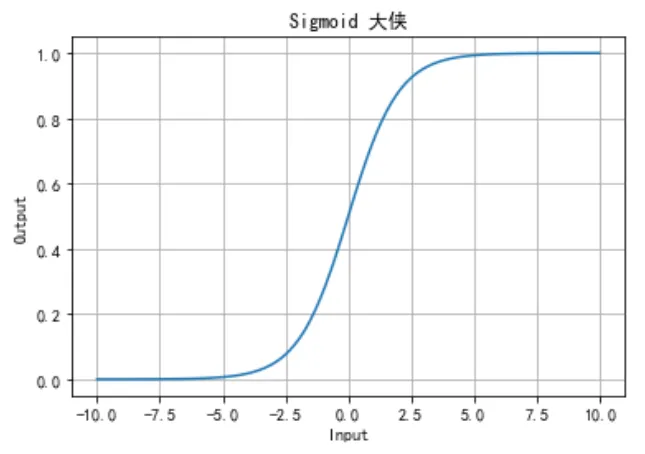
Sigmoid 函数将任意实数映射到 (0, 1) 之间，非常适合用于表示概率。

再次，直观的感受下，逻辑回归这个神奇的过程

2.4 理解分类目标

预测和实际的对比

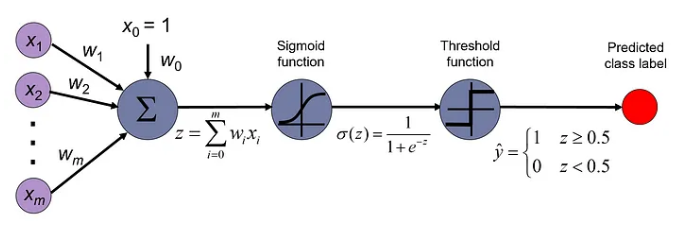
在使用逻辑回归进行分类时，核心目标是确保模型的预测概率尽可能接近实际的标签。例如，如果一个样本的实际标签是 1（正类），逻辑回归模型预测这个样本属于正类的概率应该接近 1。相反，如果样本的标签是 0（负类），则模型的预测概率应接近 0。这种方式帮助我们评价和优化模型的性能，确保模型能够正确区分不同类别的样本。

2.5 最大似然估计

最大似然估计（MLE）是一种在统计模型中估计参数的方法，它寻找能够使观测到的数据出现概率最大的参数值。在逻辑回归中，MLE尝试找到一组参数，使得给定参数下，观测到的样本标签的概率最大化。这通常通过优化一个称为似然函数的表达式来实现，该函数是对所有数据点的预测概率的乘积。

2.6 交叉熵损失

交叉熵损失函数解释

交叉熵损失函数是评估逻辑回归模型性能的一个关键工具。它衡量的是模型预测的概率分布与实际标签的概率分布之间的差异。公式可以表示为：

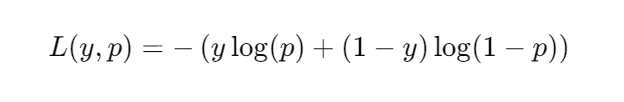
其中 ( y ) 是实际标签，( p ) 是预测为正类的概率。这个损失函数的值越小，表示模型的预测结果与实际情况越接近。

损失函数与预测准确度的关系

一般来说，交叉熵损失函数的值越小，模型的分类准确度越高。通过训练过程中损失函数的下降趋势，我们可以观察到模型性能的改善。实际操作中，可以通过绘制训练周期与损失值的图表来直观展示这一过程，帮助理解模型优化的效果。

3. 模型构建

3.1 数据准备与预处理

在构建 Logistic 回归模型之前，数据的准备和预处理是关键步骤。包括：

数据清洗：处理缺失值和异常值。
特征选择：选择与目标变量相关的特征。
数据标准化：将特征缩放到相同的范围内，以提高模型的收敛速度。

示例代码：

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 生成一个武侠主题的数据集
data = {
    '内力': [80, 60, 70, 90, 85, 75],
    '轻功': [85, 75, 65, 95, 80, 70],
    '武器': [1, 0, 1, 0, 1, 0],  # 1 表示有武器，0 表示无武器
    '是否胜利': [1, 0, 1, 1, 1, 0]  # 1 表示胜利，0 表示失败
}
df = pd.DataFrame(data)

# 特征和标签
X = df[['内力', '轻功', '武器']]
y = df['是否胜利']

# 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

3.2 模型假设与参数估计

Logistic 回归假设特征与目标变量之间存在线性关系，通过 Sigmoid 函数进行非线性变换。参数估计通过最大化对数似然函数来实现。

3.3 梯度下降法模型优化

算法原理

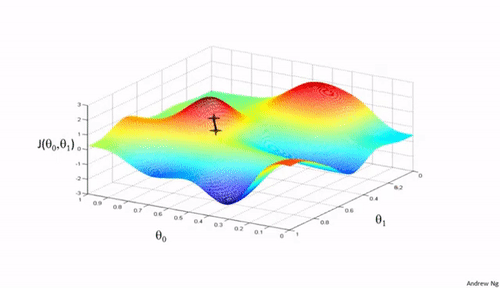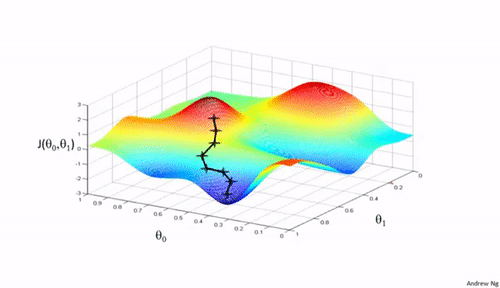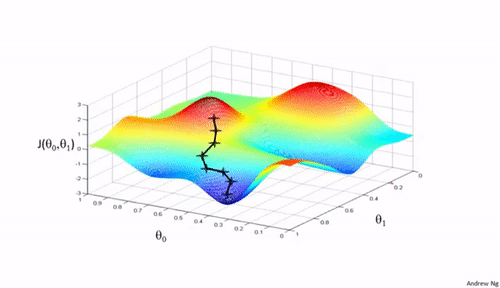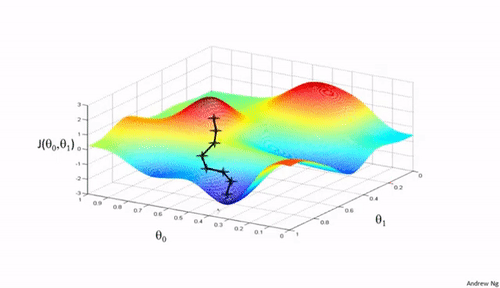
梯度下降法是一种用于优化逻辑回归模型参数的流行算法，其核心思想是利用函数的梯度（或斜率）来确定参数更新的方向。梯度指示了函数增长最快的方向，因此在优化过程中，我们沿着梯度的相反方向（下降最快的方向）调整参数，以寻找函数的最小值。

梯度下降可以通过一个简单的比喻来理解：想象你在山上，需要找到下山的最快路径。在任何位置，你都可以查看周围最陡峭的下坡路，然后朝那个方向迈出一步。梯度下降法就是这样在参数空间中寻找损失函数最小值的方法。

算法步骤

梯度下降的每一步都需要计算损失函数关于每个参数的梯度，然后用以下公式更新参数：

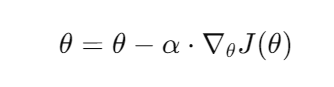
其中：

( θ ) 表示模型参数。
( α ) 是学习率，控制步长的大小。

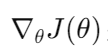
是损失函数 ( J ) 关于参数 ( θ ) 的梯度

更新的步骤重复进行，直到满足停止条件，例如梯度的大小小于某个阈值，或达到预定的迭代次数。

在实际操作中，选择合适的学习率是非常关键的，因为太小的学习率会导致收敛过慢，而太大的学习率则可能导致跳过最小值点，使得算法无法正确收敛。

4. 模型评估

4.1 混淆矩阵

混淆矩阵是一种用于评估分类模型性能的工具，它展示了预测结果与实际标签的对比情况。混淆矩阵包括以下四个指标：

TP（True Positive）：真实为正类，预测为正类。
TN（True Negative）：真实为负类，预测为负类。
FP（False Positive）：真实为负类，预测为正类。
FN（False Negative）：真实为正类，预测为负类。

示例代码：

from sklearn.metrics import confusion_matrix

# 预测
y_pred = model.predict(X_test)

# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
print(f'混淆矩阵:\n{cm}')

4.2 精度、召回率与 F1 值

精度（Precision）、召回率（Recall）和 F1 值是评价分类模型的重要指标：

示例代码：

from sklearn.metrics import precision_score, recall_score, f1_score

precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)

print(f'精度: {precision}')
print(f'召回率: {recall}')
print(f'F1 值: {f1}')

4.3 ROC 曲线与 AUC 值

ROC 曲线（Receiver Operating Characteristic Curve）展示了模型在不同阈值下的性能表现。AUC 值（Area Under Curve）是 ROC 曲线下的面积，用于衡量模型的区分能力。

示例代码：

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc

# 预测概率
y_prob = model.predict_proba(X_test)[:, 1]

# 计算 ROC 曲线
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)

# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC 曲线 (面积 = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
plt.title('接收者操作特征曲线 (ROC)')
plt.legend(loc='lower right')
plt.show()

通过这些指标和可视化方法，我们可以全面评估 Logistic 回归模型的性能。在下一部分中，我们将通过一个实际示例来展示如何使用 Python 构建和评估 Logistic 回归模型。`

5. 实战示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, accuracy_score, recall_score, f1_score, roc_curve, auc
from sklearn.model_selection import train_test_split

# 生成模拟数据
X, y = make_classification(n_samples=300, n_features=2, n_informative=2, n_redundant=0,
                           n_clusters_per_class=1, flip_y=0.01, random_state=42)

# 分割数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 使用逻辑回归进行分类
model = LogisticRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
y_prob = model.predict_proba(X_test)[:, 1]

# 计算混淆矩阵、精度、召回率和 F1 值
cm = confusion_matrix(y_test, y_pred)
accuracy = accuracy_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)

# 打印混淆矩阵和其他指标
print("混淆矩阵:\n", cm)
print("精度:", accuracy)
print("召回率:", recall)
print("F1 值:", f1)

# 可视化数据和决策边界
plt.figure(figsize=(10, 6))
plt.scatter(X_test[y_test == 0][:, 0], X_test[y_test == 0][:, 1], color='red', label='类别 0', edgecolor='k')
plt.scatter(X_test[y_test == 1][:, 0], X_test[y_test == 1][:, 1], color='blue', label='类别 1', edgecolor='k')

# 绘制决策边界和填充区域
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                     np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.2, cmap=plt.cm.Paired)
plt.contour(xx, yy, Z, levels=[0.5], linestyles='dashed', colors='black')

plt.title('武侠世界中的高手分类图')
plt.xlabel('功力')
plt.ylabel('内功心法')
plt.legend()
plt.show()

# 计算并可视化 ROC 曲线
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)

plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC 曲线 (面积 = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假阳性率')
plt.ylabel('真阳性率')
plt.title('受试者工作特征 (ROC) 曲线')
plt.legend(loc="lower right")
plt.show()

运行后输出：

混淆矩阵:
 [[44  2]
 [ 2 42]]
精度: 0.9555555555555556
召回率: 0.9545454545454546
F1 值: 0.9545454545454546

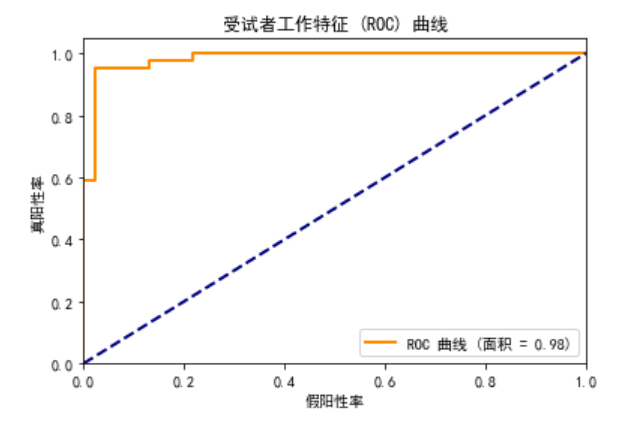
这张图展示了模型在不同阈值下的性能：

X 轴表示假阳性率（False Positive Rate, FPR），即被错误预测为正类的负类样本的比例。
Y 轴表示真阳性率（True Positive Rate, TPR），即被正确预测为正类的正类样本的比例。
曲线表示模型在不同阈值下的表现。
对角线（从 (0, 0) 到 (1, 1) 的虚线）表示随机猜测的表现。

曲线越接近左上角，模型的性能越好。在这次运行中，曲线下的面积（AUC）为 0.98，表示模型在区分正负类样本时具有很高的性能。很强大

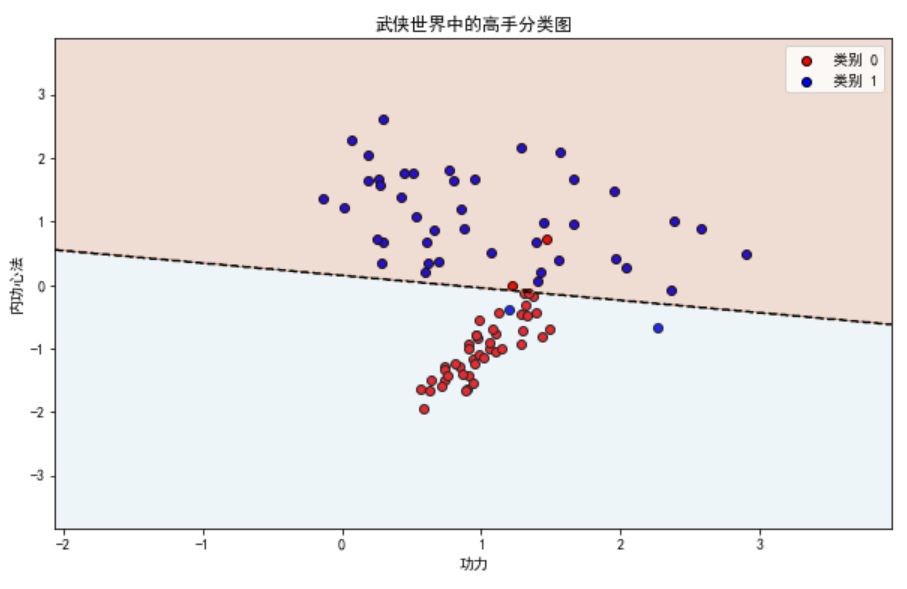
这张图展示了测试数据点及其分类结果：

红色点代表类别 0（例如低等级武侠高手）。
蓝色点代表类别 1（例如高等级武侠高手）。
黑色虚线表示模型的决策边界，划分了类别 0 和类别 1 的区域。
背景颜色：决策边界两侧的背景颜色不同，用于区分类别。左侧区域（通常是类别 0）为浅红色，右侧区域（通常是类别 1）为浅蓝色。

这张图展示了模型如何基于两个特征（功力和内功心法）对数据点进行分类。大部分数据点都被正确分类，但也有少量数据点被误分类，这些误分类的数据点位于决策边界附近。再次，强大

6. 进阶话题

6.1 正则化与过拟合

在 Logistic 回归中，正则化是一种防止过拟合的技术。过拟合是指模型在训练集上表现良好，但在测试集上表现不佳。正则化通过在损失函数中加入惩罚项来减少模型的复杂度，从而提高模型的泛化能力。

L1 正则化（Lasso）：通过增加参数绝对值之和的惩罚项，使部分参数变为零，达到特征选择的效果。
L2 正则化（Ridge）：通过增加参数平方和的惩罚项，使得所有参数趋近于零，但不会完全为零。

示例代码：

# 使用 L1 正则化
model_l1 = LogisticRegression(penalty='l1', solver='liblinear')
model_l1.fit(X_train, y_train)

# 使用 L2 正则化
model_l2 = LogisticRegression(penalty='l2')
model_l2.fit(X_train, y_train)

print(f'L1 正则化模型系数: {model_l1.coef_}')
print(f'L2 正则化模型系数: {model_l2.coef_}')

6.2 多分类问题中的 Logistic 回归

Logistic 回归不仅可以用于二分类问题，也可以扩展到多分类问题。在多分类问题中，常用的方法有：

一对多（One-vs-Rest, OvR）：为每个类别训练一个二分类器，每个分类器区分该类别与其他类别。
一对一（One-vs-One, OvO）：为每对类别训练一个二分类器，总共训练 ?(?−1)2?(?−1)2 个分类器，其中 ?? 是类别数量。

示例代码：

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# 生成多分类数据集
X, y = make_classification(n_samples=100, n_features=4, n_classes=3, n_clusters_per_class=1, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练多分类 Logistic 回归模型（OvR）
model_ovr = LogisticRegression(multi_class='ovr')
model_ovr.fit(X_train, y_train)

# 训练多分类 Logistic 回归模型（softmax）
model_softmax = LogisticRegression(multi_class='multinomial', solver='lbfgs')
model_softmax.fit(X_train, y_train)

print(f'OvR 模型系数: {model_ovr.coef_}')
print(f'Softmax 模型系数: {model_softmax.coef_}')

6.3 与其他分类算法的对比

Logistic 回归虽然简单，但在某些情况下可能不如其他复杂的分类算法，如支持向量机（SVM）、随机森林和神经网络。对比这些算法的优缺点：

支持向量机（SVM）：在高维空间中寻找最优分类超平面，适用于复杂的数据集，但计算复杂度高。
随机森林：集成多棵决策树，提高模型的准确性和稳定性，但解释性差。
神经网络：强大的非线性建模能力，适用于大规模数据，但训练时间长且需要大量计算资源。

示例代码：

from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# 训练 SVM 模型
svm_model = SVC()
svm_model.fit(X_train, y_train)
svm_pred = svm_model.predict(X_test)
svm_accuracy = accuracy_score(y_test, svm_pred)

# 训练随机森林模型
rf_model = RandomForestClassifier()
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)
rf_accuracy = accuracy_score(y_test, rf_pred)

# 训练神经网络模型
nn_model = MLPClassifier(max_iter=1000)
nn_model.fit(X_train, y_train)
nn_pred = nn_model.predict(X_test)
nn_accuracy = accuracy_score(y_test, nn_pred)

print(f'SVM 准确率: {svm_accuracy}')
print(f'随机森林准确率: {rf_accuracy}')
print(f'神经网络准确率: {nn_accuracy}')

通过这些进阶话题的介绍，大侠们可以更全面地理解 Logistic 回归及其在不同场景下的应用与对比。