
我们提供安全,免费的手游软件下载!
记得是在 2015 看到过的一个 html5 演示效果, 很惊艳
当时没明白如何实现,现在我会了,做一个类似的:

又弄了一个拖动的 demo
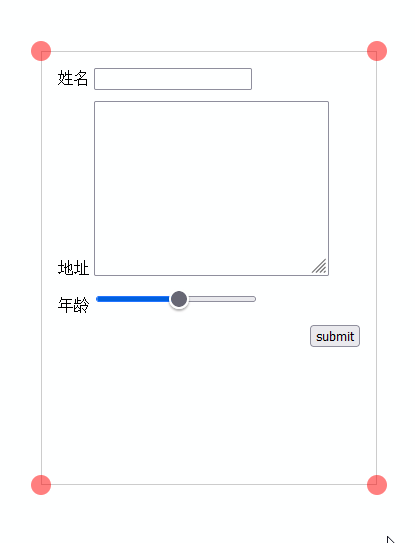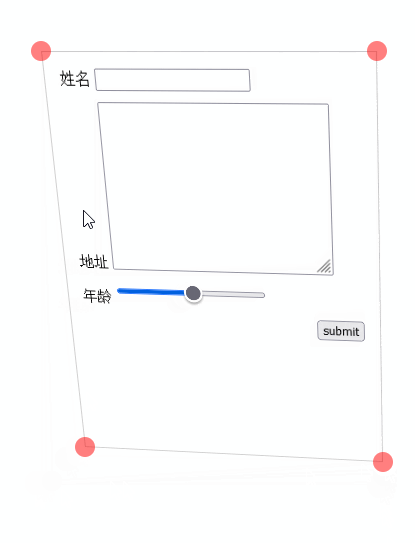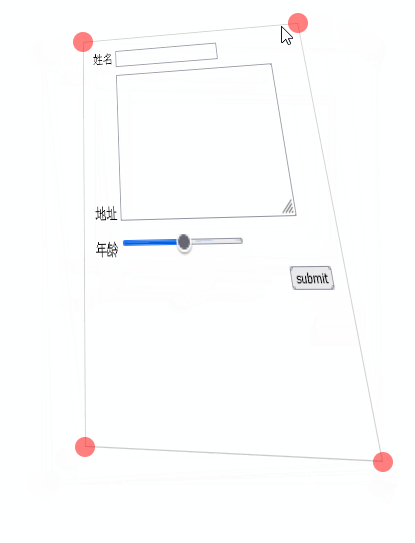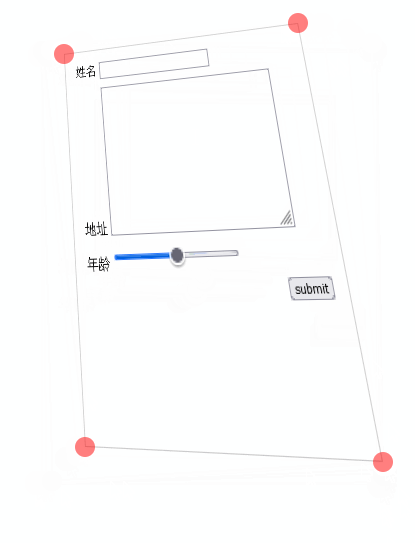
“你好老师!学这个矩阵具体有什么用?”
老师喝着水貌似想了一会儿回答:“考试用”..
这个问题我真问过老师
在校期间数学课上学到矩阵行列式相关的课程时,曾经问过当时的数学老师,学这个做啥用的,老师犹豫了半天给我的答案是 “考试用”
果然.. 最后我的成绩是不及格
当然不能怪老师,我本来的数学成绩一直也是垫底的
对于我这样的学渣来说,学习不能学以致用就像玩的游戏没有及时正反馈一样的难受
我是真的很难提起兴趣去学
为啥选了前端开发这个坑呢?就是因为代码写了刷新一下浏览器就能看到效果,真实时反馈
直到工作多年以后,学到图形学相关的知识才一知半解
为啥是一知半解呢,因为知道有这个东西,也知道用在哪里,可就是不会用,至少在大部分的前端开发工作上用不到
能在网上找到的相关应用就是 css 中利用 transform 对某个元素进行 旋转,平移,缩放,倾斜等, 这些基础应用都被讲烂了
像这样:
.box {
transform-origin:0 0;
transform: rotate(10deg) translateX(30px) scale(1.1, 1.1) skew(3deg, 3deg);
}

transform 后:

但你应该明白它最终是以矩阵形式表达的,八股文中有没有要背的我不知道,毕竟这些知识很多人已经讲过了。当然如果你这都不知道,可能八股还得再八股一下
通过火狐的开发者工具查看 computed 面板中可以看到其实转换成了对应的 matrix
结果 matrix:

线性变幻 linear transform 包括以下几种
用矩阵形式表达如下图示:
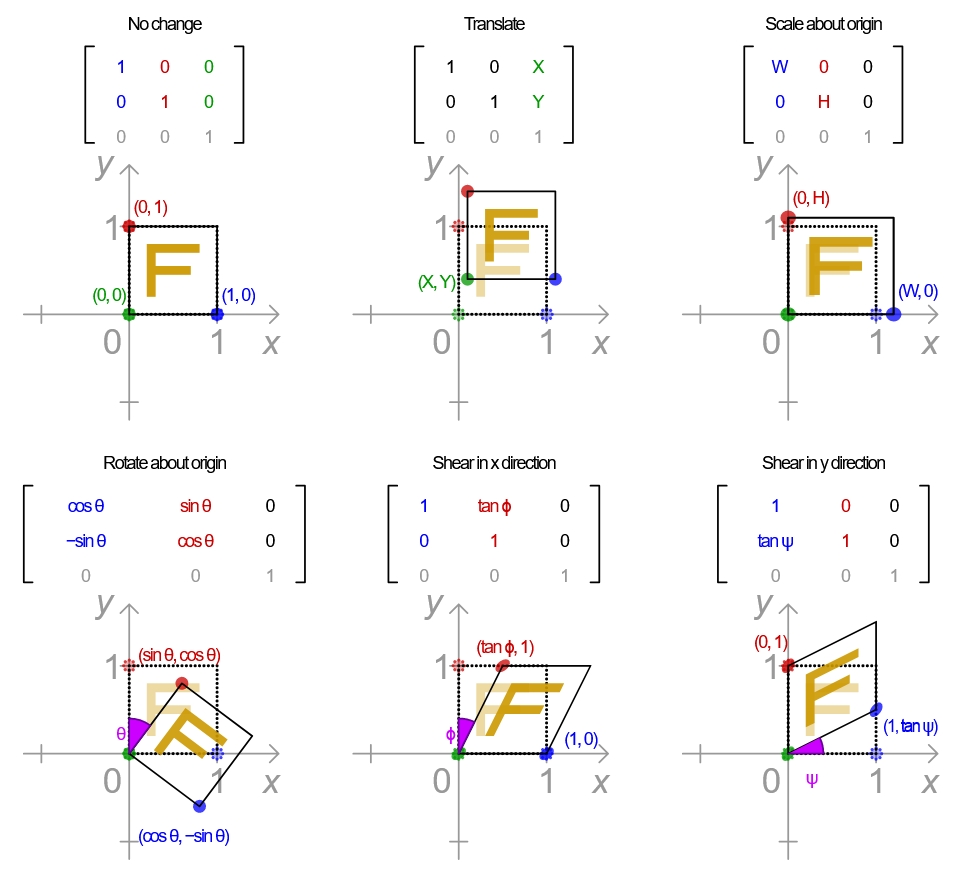
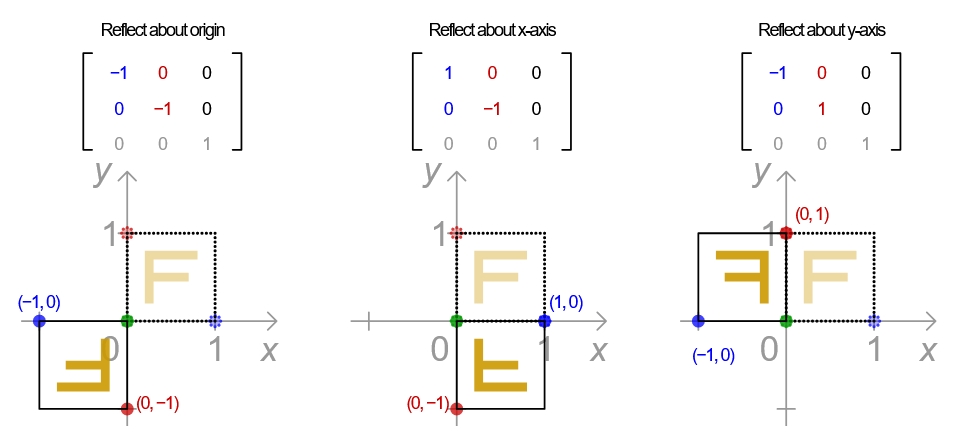
这些都可以组合在一起形成 单个 matrix 矩阵实现变幻,
这在之前的我的 "EaselJS 源码分析系列--第二篇" 中有提到过,宽高,旋转,斜切,转换成 matrix 后一次变幻到位
拿上面的例子举例: 实质是对绿色 box 四个坐标 (0,0)、(200,0)、(0,200)、(200,200) 分别点乘了 (Dot product) matrix 矩阵:
matrix(1.07328, 0.247786, -0.13424, 1.0933, 29.5442, 5.20945)
得到新坐标:
(29,5), (244.2002, 54.76665), (2.6962, 223.86945), (217, 273)

怎么点乘?
说到点乘简单复习一下大学数学基础知识(看看就行了,你不需要自己算)
2 · 2
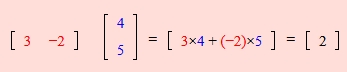
3 · 3
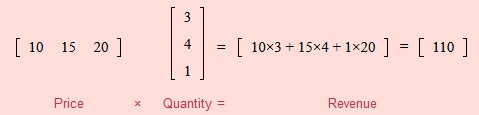
虽然你不用自己算,但 matrix 函数参数得搞明白
注意函数 matrix 参数 a, b, c, d, tx, ty 对应的位置:
matrix(a, b, c, d, tx, ty)
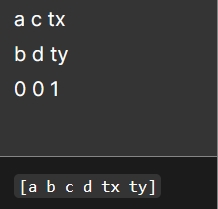
手动计算是不可能的我们可以使用 numeric.js 数学库用于点乘计算:
// 在 numeric.dot 中的位置
numeric.dot([
[a, c, tx],
[b, d ty],
[0, 0, 1]
]
, [0, 0, 1]
)
这是上面四个坐标的计算:
// matrix(1.07328, 0.247786, -0.13424, 1.0933, 29.5442, 5.20945);
// 位置 (0, 0)
const pos1 = numeric.dot([
[1.07328, -0.13424, 29.5442],
[0.247786, 1.0933, 5.20945],
[0, 0, 1]]
, [0, 0, 1])
// 位置 (200 ,0 )
const pos2 = numeric.dot([
[1.07328, -0.13424, 29.5442],
[0.247786, 1.0933, 5.20945],
[0, 0, 1]]
, [200, 0, 1])
// 位置 (0, 200)
const pos3 = numeric.dot([
[1.07328, -0.13424, 29.5442],
[0.247786, 1.0933, 5.20945],
[0, 0, 1]]
, [0, 200, 1])
// 位置 (200, 200)
const pos4 = numeric.dot([
[1.07328, -0.13424, 29.5442],
[0.247786, 1.0933, 5.20945],
[0, 0, 1]]
, [200, 200, 1])
console.log(pos1, pos2, pos3, pos4)
// (29,5), (244.2002, 54.76665), (2.6962, 223.86945), (217, 273)
再仔细想想,想要仿射变换直接使用 matrix 是符合直觉的
旧坐标 · matrix = 新坐标
所以想要自由就得用到 matrix
先要进行亿点点线性代数运算
我们现在给四个角(坐标点)对应编号(“旧坐标”):
(x1,y1), (x2,y2) , (x3,y3) , (x4,y4)
目的是将它们映射(变幻)到对应的(“新坐标”):
(u1,v1), (u2,v2) , (u3,v3) , (u4,v4)
即将坐标 (x i , y i ) 映射到 (u i , v i )
坐标 (x, y) 被表示为 (kx, ky, k), k 不为 0
在齐次坐标中 (3,2,1) 和 (6,4,2) 都可以表示 (3,2)
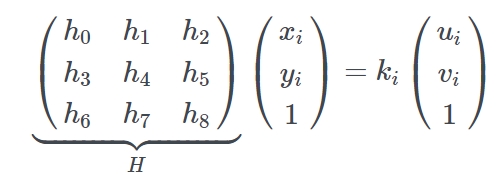
于是我们要求得转置矩阵 H 要满足上面等式中所有已知的角 (x i , y i ), (u i , v i )
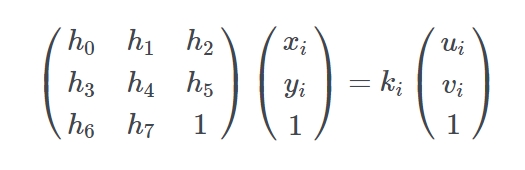
满足 H 的值不是唯一的,举例,给 H 缩放乘以一个常数,结果矩阵依然会映射对应的点(右侧的 k i 也是一样的)
为了简化问题设假定将两边都缩放直到 h8 为 1 (简化问题计算)
然后将乘数乘进去
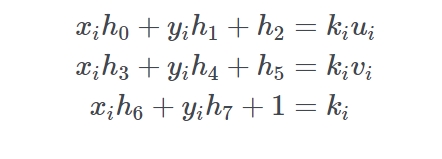
现在将第3行等式代入前两行把 k i 去掉先
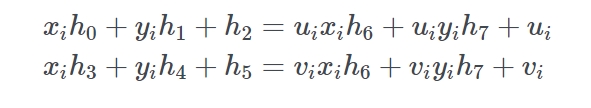
记住我们要解决的是 h i 所以我们应该尝试先把它们分开来
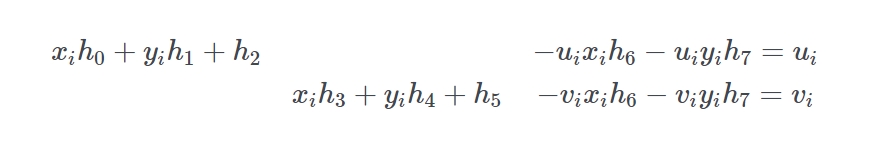
两个等式中 h0..h7 空出缺少的部分用 0 填充 (为何要填充:H 等于 k i 若要等式相等则 H 必须是 h0..h7 完整)
将 h 提出来来,用矩形形式表示就是:

由于我们要表示的是四个坐标点的映射,所以我们可以写成这样:

至此已经可以了,就是一个 Ah=b 的问题(即矩阵中常见的 Ax=b),可以用线性代数库(比如:numeric.js 的 numeric.solve)来求解 h ,解得的 h 对应的 h i 用于 transform 形变矩阵
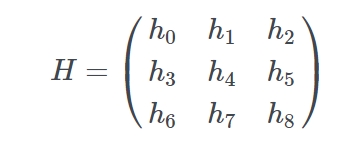
最后一个小问题,就是 Matrix3d 需要的是 4x4 的矩阵,我们从开始就忽略掉了 z 轴值(由于四个点都在同一个平面,所以 z = 0), 所以把 z 重新映射回矩阵
matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1)
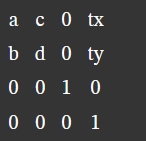
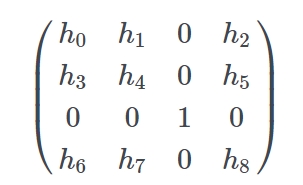
这就是最后用于 css 上的 matrix3d 的矩阵
创建一个 id 为 box 的 div 作为变化源
创建一个 id 为 targetBox 的 div 作为目标
创建一个 getPoints 用于获取四个点坐标
... 省略获取 targetBox,box 的代码
function getPoints(element){
const rect = element.getBoundingClientRect();
return [
[rect.left, rect.top],
[rect.left, rect.bottom],
[rect.right, rect.top],
[rect.right, rect.bottom],
];
}
const target = getPoints(targetBox)
const origin = getPoints(box)
分别转换成相对坐标点
function getFromPoints(points){
// 映射前四个点相对坐标
const result = [];
const len = points.length;
for (let k = 0; k < len; k++) {
let p = points[k];
result.push({
x: p[0] - points[0][0],
y: p[1] - points[0][1]
});
}
/**
result
[
{x1, y1},
{x2, y2},
{x3, y3},
{x4, y4},
]
*/
return result;
}
function getToPoints(origin, target){
// 映射后四个点相对坐标
const result = [];
for (let k = 0, len = target.length; k < len; k++) {
p = target[k];
result.push({
x: p[0] - origin[0][0],
y: p[1] - origin[0][1]
});
}
return result;
}
const from = getFromPoints(origin);
const to = getToPoints(origin, target);
通过 from 与 to 获取 H
function getTransform(from, to) {
var A, H, b, h;
A = []; // 8x8
// 四个点的坐标
for (let i =0 ; i < 4; i++) {
A.push([from[i].x, from[i].y, 1, 0, 0, 0, -from[i].x * to[i].x, -from[i].y * to[i].x]);
A.push([0, 0, 0, from[i].x, from[i].y, 1, -from[i].x * to[i].y, -from[i].y * to[i].y]);
}
b = []; // 8x1
for (let i = 0; i < 4; i++) {
b.push(to[i].x);
b.push(to[i].y);
}
// Solve A * h = b for h
// 即矩阵中常见的 Ax=b
// numeric.solve eg:
// IN> numeric.solve([[1,2],[3,4]],[17,39])
// OUT> [5,6]
// https://ccc-js.github.io/numeric2/documentation.html
h = numeric.solve(A, b);
/**
解得: h matrix
[
h0, h1, 0 h2
h3, h4, 0 h5
0, 0, 0, 1
h6, h7, 0 h8
]
*/
H = [
[h[0], h[1], 0, h[2]],
[h[3], h[4], 0, h[5]],
[0, 0, 1, 0],
[h[6], h[7], 0, 1]
];
return H;
};
const H = getTransform(from, to);
生成 css 值应用到 div 上
function getMatrixCSSParameters(H){
// 获取 css matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1) 参数
const result = [];
for (let i =0; i < 4; i++) {
const result1 = [];
for (let j = 0; j < 4; j++) {
result1.push(H[j][i].toFixed(20));
}
result.push(result1);
}
return result.join(',');
}
div.style.transform = `matrix3d(${getMatrixCSSParameters(H)})`;
走了一大圈,现在终于可以实现“仿射变换”了
demo 1 matrix3d 动画变化
https://github.com/willian12345/blogpost/blob/main/matrix/free-css-3d-transform/transform3d.html
demo 2 matrix3d 四角拖动变化
https://github.com/willian12345/blogpost/blob/main/matrix/free-css-3d-transform/drag.html
我们碰到的问题大概率编程的前辈们都碰到过了
通过搜索后发现“仿射变换” 在 opencv 中有现成的函数
const H = cv.getPerspectiveTransform(from, to);
然后就 github 上找了一下,果然是有人实现了
然后用它提供的函数实现一遍 demo2
https://github.com/willian12345/blogpost/blob/main/matrix/free-css-3d-transform/drag-perspective-transform.html
参考资料
https://developer.mozilla.org/zh-CN/docs/Web/CSS/transform-function/matrix
https://angrytools.com/css-generator/transform/
https://franklinta.com/2014/09/08/computing-css-matrix3d-transforms/
https://docs.opencv.org/2.4/modules/imgproc/doc/geometric_transformations.html#getperspectivetransform"
https://www.zweigmedia.com/RealWorld/tutorialsf1/frames3_2.html
https://ccc-js.github.io/numeric2/
https://github.com/fccm/getPerspectiveTransform
注:转载请注明出处博客园:王二狗Sheldon池中物 (willian12345@126.com)
热门资讯