我们提供安全，免费的手游软件下载！

安卓手机游戏下载_安卓手机软件下载_安卓手机应用免费下载-先锋下载

当前位置: 主页 > 软件教程 > 软件教程

Google相机 正版 Google相机 正版 漫酷阅读器 官网下载安装手机版 漫酷阅读器 官网下载安装手机版 漫酷阅读器 免费下载 漫酷阅读器 免费下载 多看阅读 app官方版 多看阅读 app官方版 拷贝漫画 app官网入口2024版 拷贝漫画 app官网入口2024版 kuyo加速器 官方免费下载版 kuyo加速器 官方免费下载版 DNF助手 2025最新版 DNF助手 2025最新版 次元盒子 次元盒子 迅猛兔加速器 免费下载入口 迅猛兔加速器 免费下载入口 迅猛兔加速器 2025最新版 迅猛兔加速器 2025最新版

记录一次物理专业编程大作业完成过程

来源：网络 更新时间：2024-08-13 09:33:29

起因

有一天毕业多年的大学同学在班级微信群里问有没有人能帮忙写一段代码实现一个功能

然后贴了一段要实现的要求

我一看这段描述简直就头大了，程序员都比较害怕这种没有格式的文字，甚至连个换行都没有，说实话多看一眼就感觉莫名烦躁。我也就没敢讲话，即使有同学在群里已经开始点名了，也始终一言不发。

找上门

后来同学就直接找上我了，虽然毕业后交集很少，但是大学时关系还是蛮不错的，所以就答应了。

然后他说明了一下，是他读大学的弟弟的课程大作业，他弟弟学的是物理专业，要求用编码完成一个物理作业。发过来一个文档比较详细的说明了物理作业的内容。
物理大作业：

这个文档其实我也看的一头雾水，第一是自从高中毕业之后就没学过物理了，理解起来有点吃力；第二是看不懂所以很多物理知识不能抽象成编程代码的逻辑。

理解需求

结合他之前发的文档和他弟弟的多次沟通，先把需求弄明白了。

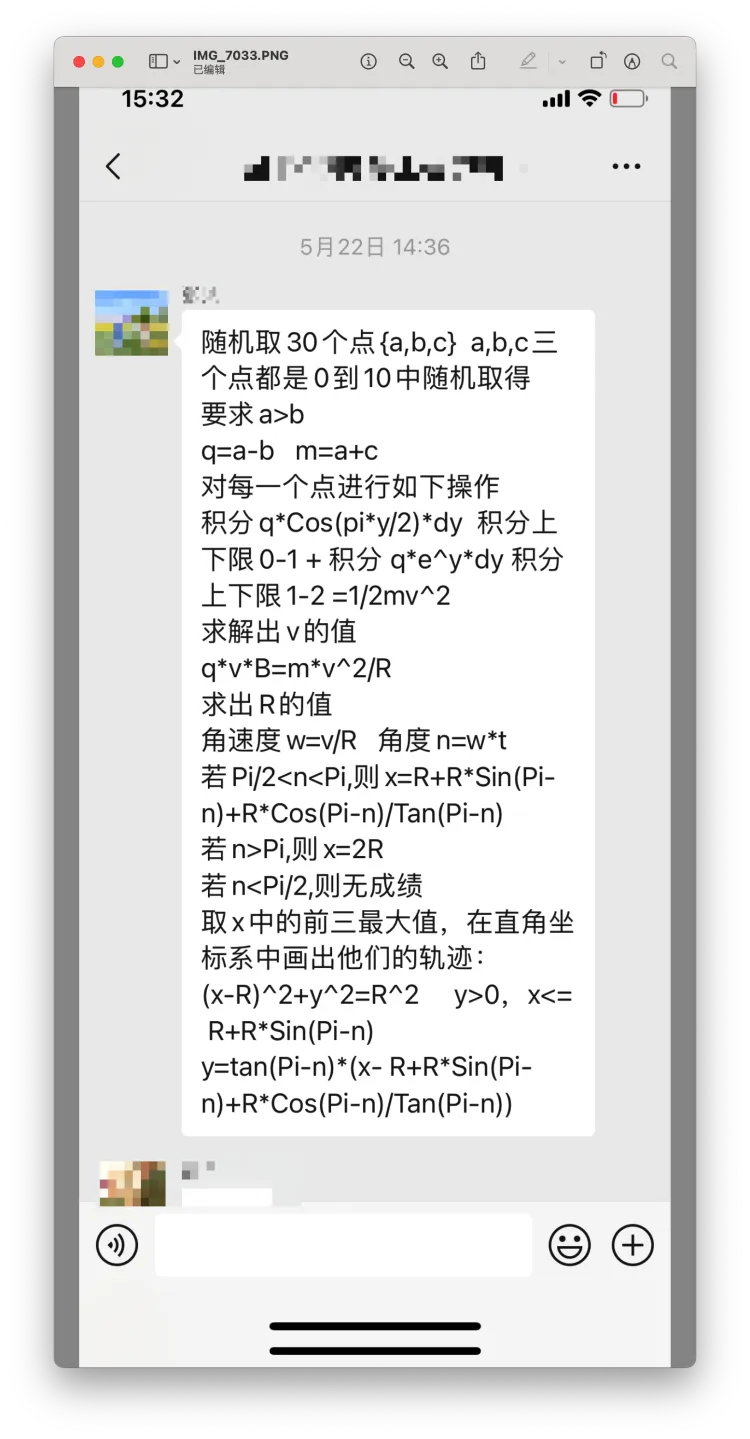
简单来说就是如下：

随机取30个点{a,b,c} a,b,c三个点都是0到10中随机取得
要求a>b
q=a-b m=a+c
对每一个点进行如下操作

已知：
积分q Cos(pi y/2) dy 积分上下限0-1 + 积分 q e^y*dy 积分上下限1-2 = 1/2mv^2
问题一 ：求解出v的值

已知：
q v B=m*v^2/2R
问题二 ：求出R的值

已知：
角速度w=v/R 角度n=w t
若Pi/2 Sin(Pi-n)+R*Cos(Pi-n)/Tan(Pi-n)
若n>Pi,则x=2R
若n 问题三 ：取x中的前三最大值。

问题四 ：
在直角坐标系中画出他们的轨迹：
(x-R) 2+y 2=R^2
y>0，x<= R+R Sin(Pi-n)
y=tan(Pi-n) (x- R+R Sin(Pi-n)+R Cos(Pi-n)/Tan(Pi-n))

到这里总算搞明白了需求是什么了，程序员最怕需求不明确，而且遇到水平不行的产品经理，真是遭老罪了。

物理问题转化成数学问题

虽然搞明白了需求是什么，但是让我回忆高中物理知识并正确解答出来也是力不能及的事情。高中时期上知天文下知地理，中间知物理，现在只知道爱理不理。我擅长的是把公式用代码表达出来，要是公式都没有，我也搞不定。

然后我就让他用把物理题做一遍，有了做题的过程，我就好转换成代码了。很快啊，他就把解题过程给我发过来了。

其中涉及到一些积分的运算，我努力回想多年前学习过的微积分，在记忆的深处找到一些答案。

最后整理出各个问题的解答方式：
问题一 ：求解出v的值 ，v的计算公式如上
问题二 ：求出R的值，R的计算公式如上
问题三 ：取x中的前三最大值。
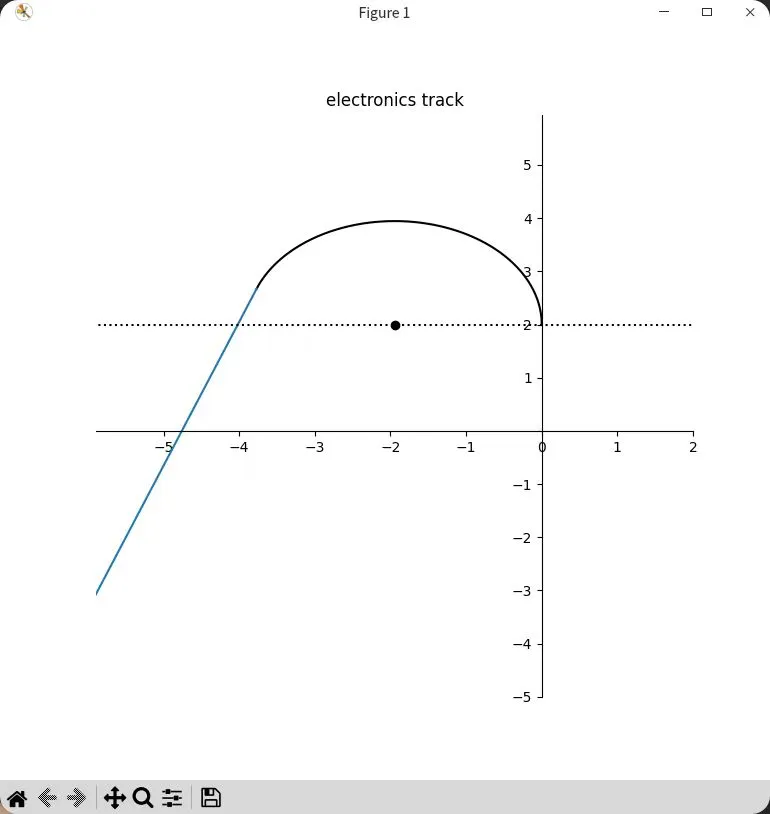
问题四 ：在直角坐标系中画出他们的轨迹

写代码

下面就是写代码解决以上问题。知道了解答的过程和公式，接下来就是写代码的过程。

毫无疑问python是最合适完成这个工作的语言，考虑到他的编码基础，我要求自己写的代码 结构清晰 ， 注释清楚 ， 函数短小 ， 变量明确 ， 不炫技 ， 不使用高级数据结构 。

生成30个随机数 

def gen_30_point():
    """生成30个随机数，3个为一组"""
    point_list = []

    while len(point_list) < TOTAL:
        a = random.randint(0, 10)
        b = random.randint(0, 10)

        # 要求a必须大于b，生成随机数如果a小于等于b，则丢弃该组数据
        if a <= b:
            continue

        c = random.randint(0, 10)
        point_list.append((a, b, c))

    return point_list

根据随机数计算出电荷量和电子质量 

def calculate_q_m(point_list):
    """根据a,b,c计算出q，m"""
    q_m_list = []
    for a, b, c in point_list:
        q = (a - b) * ELECTRON_CHARGE
        m = (a + c) * ELECTRON_QUALITY
        q_m_list.append((q, m))
    return q_m_list

轻松计算出问题一的v 


def calculate_v(q, m):
    """计算出速度v"""
    v = 2 * q * (2 / PI + E ** 2 - E) / m
    v = math.sqrt(v)
    return v

计算出问题二的R 

def calculate_r(q, m, v):
    """计算出半径R"""
    r = m * v / (2 * B * q)
    return r

计算出问题三的x 


def calculate_x(n, r):
    """计算出x"""
    x = 0

    if n > PI:
        x = 2 * r
    elif n < PI / 2:
        x = 0
    else:
        x = r + r * math.sin(PI-n) + r * math.cos(PI-n)/math.tan(PI-n)

    return x

解决问题四的直角坐标系下的图形 


def draw_track(n, r):
    # 设置圆的参数
    radius = r  # 半径
    circle_center = (-r, 2)  # 圆心坐标，例如(2, 3)
    # 生成圆的x和y坐标
    theta = np.linspace(0, n, 100)  # 生成0到2π的100个点
    x = circle_center[0] + radius * np.cos(theta)
    y = circle_center[1] + radius * np.sin(theta)
    # 绘制圆
    plt.plot(x, y, "k")
    # 标记圆心
    plt.plot(circle_center[0], circle_center[1], 'ko')  # 蓝色圆点标记圆心
    # 设置坐标轴范围
    plt.xlim(circle_center[0] - radius - 2, circle_center[0] + radius + 2)
    plt.ylim(circle_center[1] - radius - 2, circle_center[1] + radius + 2)

    # 直线
    x = np.linspace(-30, x[-1], 20)
    y = -x / math.tan(n) + r * math.sin(n) + 2 - r / math.tan(n) + r * math.cos(n) / math.tan(n)
    plt.plot(x, y)

    # y = 2 横线
    x = np.linspace(-4 * r, 2 * r, 10)
    y = np.array([2] * len(x))
    plt.plot(x, y, "k:")

    # 坐标系
    new_ticks = np.linspace(-5, 5, 11)
    plt.yticks(new_ticks)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')

    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))

    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    # 隐藏掉y轴的0坐标，不然和x轴重了，不好看，0位于从下到上第6个
    yticks = ax.yaxis.get_major_ticks()
    yticks[5].label1.set_visible(False)

    # 设置坐标轴标题
    plt.title('electronics track')

    # 显示图形
    plt.show()

在绘制直角坐标系时发现这个公式存在问题，于是和他讨论沟通

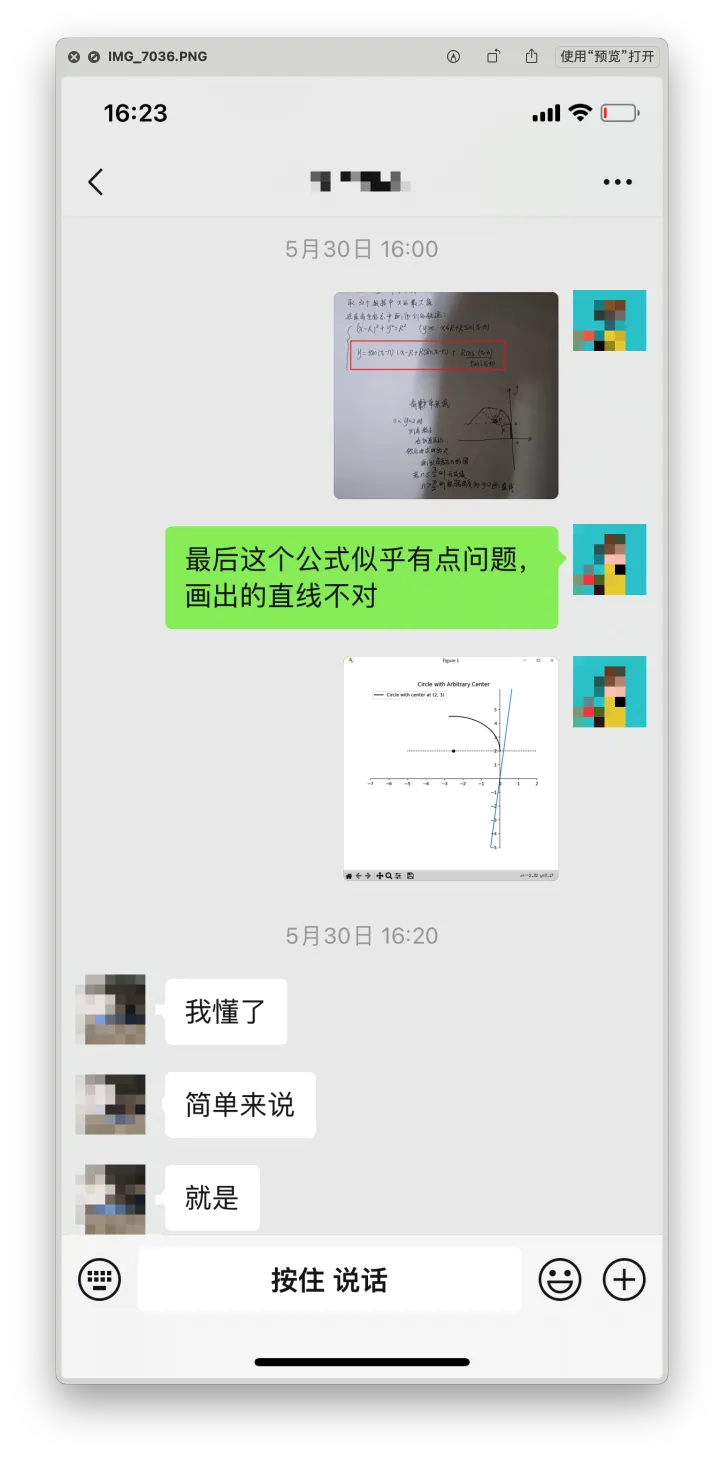
最终的效果

最后他拿着代码在期末完成了作业的讲演，顺利过关。

小结

可以从过程中看到，写代码的难度不高，主要是前期理解难度大，不管是物理知识，还是微积分在日常项目开发中真的很少见，更多的是API接口，Redis，MySQL啥的。通过不断的沟通，正确理解需求，再将物理知识抽象成数学内容，最后用代码表达出来，这个过程何尝不是一次项目开发的缩影呢。
最后，赚到一顿饭?

附录完整代码 


"""

运行方法：
1. 安装依赖文件
pip3 install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple
pip3 install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple

2. 运行代码
python3 physics_code.py


题目：
步骤一： （完成）
随机取30个点{a,b,c}  a,b,c三个点都是0到10中随机取得
要求 a>b， 计算：q=a-b   m=a+c

步骤二：求出V (完成)

步骤三：求出R （完成）

步骤四：求出X，取top3 （完成）

步骤五：画出轨迹 (完成)
"""

import math
import random
import matplotlib.pyplot as plt
import numpy as np

TOTAL = 30
PI = 3.14
E = 2.71
B = 10 ** -4
T = 2 * 10 ** -4
ELECTRON_CHARGE = 1.602 * 10 ** -19
ELECTRON_QUALITY = 1.672 * 10 ** -27


def gen_30_point():
    """生成30个随机数，3个为一组"""
    point_list = []

    while len(point_list) < TOTAL:
        a = random.randint(0, 10)
        b = random.randint(0, 10)

        # 要求a必须大于b，生成随机数如果a小于等于b，则丢弃该组数据
        if a <= b:
            continue

        c = random.randint(0, 10)
        point_list.append((a, b, c))

    return point_list


def calculate_q_m(point_list):
    """根据a,b,c计算出q，m"""
    q_m_list = []
    for a, b, c in point_list:
        q = (a - b) * ELECTRON_CHARGE
        m = (a + c) * ELECTRON_QUALITY
        q_m_list.append((q, m))
    return q_m_list


def calculate_v(q, m):
    """计算出速度v"""
    v = 2 * q * (2 / PI + E ** 2 - E) / m
    v = math.sqrt(v)
    return v


def calculate_r(q, m, v):
    """计算出半径R"""
    r = m * v / (2 * B * q)
    return r


def calculate_n(v, r):
    """计算出n"""
    n = v * T / r
    return n


def calculate_x(n, r):
    """计算出x"""
    x = 0

    if n > PI:
        x = 2 * r
    elif n < PI / 2:
        x = 0
    else:
        x = r + r * math.sin(PI-n) + r * math.cos(PI-n)/math.tan(PI-n)

    return x


def draw_track(n, r):
    # 设置圆的参数
    radius = r  # 半径
    circle_center = (-r, 2)  # 圆心坐标，例如(2, 3)
    # 生成圆的x和y坐标
    theta = np.linspace(0, n, 100)  # 生成0到2π的100个点
    x = circle_center[0] + radius * np.cos(theta)
    y = circle_center[1] + radius * np.sin(theta)
    # 绘制圆
    plt.plot(x, y, "k")
    # 标记圆心
    plt.plot(circle_center[0], circle_center[1], 'ko')  # 蓝色圆点标记圆心
    # 设置坐标轴范围
    plt.xlim(circle_center[0] - radius - 2, circle_center[0] + radius + 2)
    plt.ylim(circle_center[1] - radius - 2, circle_center[1] + radius + 2)

    # 直线
    x = np.linspace(-30, x[-1], 20)
    y = -x / math.tan(n) + r * math.sin(n) + 2 - r / math.tan(n) + r * math.cos(n) / math.tan(n)
    plt.plot(x, y)

    # y = 2 横线
    x = np.linspace(-4 * r, 2 * r, 10)
    y = np.array([2] * len(x))
    plt.plot(x, y, "k:")

    # 坐标系
    new_ticks = np.linspace(-5, 5, 11)
    plt.yticks(new_ticks)
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')

    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))

    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    # 隐藏掉y轴的0坐标，不然和x轴重了，不好看，0位于从下到上第6个
    yticks = ax.yaxis.get_major_ticks()
    yticks[5].label1.set_visible(False)

    # 设置坐标轴标题
    plt.title('electronics track')

    # 显示图形
    plt.show()


if __name__ == "__main__":
    point_list = gen_30_point()
    q_m_list = calculate_q_m(point_list)

    x_list = []
    for q, m in q_m_list:
        v = calculate_v(q, m)
        r = calculate_r(q, m, v)
        n = calculate_n(v, r)
        x = calculate_x(n, r)
        x_list.append((x, n, r))
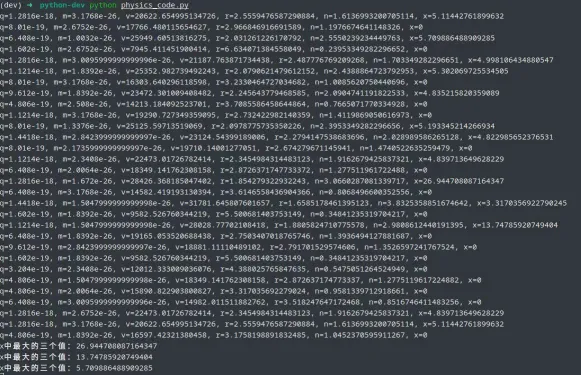
        print(f"q={q}, m={m}, v={v}, r={r}, n={n}, x={x}")

    x_list.sort(reverse=True, key=lambda i : i[0])

    for x, n, r in x_list[:3]:
        print(f"x中最大的三个值：{x}")

    for x, n, r in x_list[:3]:
        draw_track(n, r)

相关资讯

Go中数组和切片

11-14

使用鸿蒙NEXT框架开发光强仪应用

11-14

DDCA —— 内存架构和子系统&内存控制器

11-14

如何使用Spring Boot进行文件压缩处理

11-14

淘宝双12津贴领取教程

11-13

Spring AI 再更新：如何借助全局参数实现智能数据库操作与个性化待办管理

11-13

如何在OpenAI Gym中创建自定义环境

11-12

功能权限和数据权限在系统中的作用

11-11

在 Github Action 管道内集成 Code Coverage Report

11-11

Nuxt.js 应用中的 listen 事件钩子详解

11-10

热门攻略

独奏第1季评论

独奏第1季评论

  • 火之谜评论 03-23

  • MLB节目24评论 03-23

  • 部落3：竞争对手最终审查 03-20

  • Palm Royale评论 03-20

  • 大盗窃小村庄评论 03-20

    • 热门资讯

    如何使用Spring Boot进行文件压缩处理11-14

    Spring AI 再更新：如何借助全局参数实现智能数据库操作与个性化待办管理11-13

    功能权限和数据权限在系统中的作用11-11

    在 Github Action 管道内集成 Code Coverage Report11-11

    好未来：多云环境下基于 JuiceFS 建设低运维模型仓库11-09

    热门游戏

    安卓软件
    系统工具 拍照摄影 主题美化 生活服务 趣味娱乐 资讯阅读 育儿母婴 手游辅助
    安卓游戏
    射击枪战 策略塔防 休闲益智 动作闯关 冒险解谜 赛车竞速 手机网游 体育运动
    资讯
    新闻资讯 科技周边
    网站地图
    Copyright © 2007- 2023 www.91xfw.com. All Rights Reserved.苏ICP备20025626号